Combinatorial Coverage as an Estimator of Residual Risk after Testing

Abstract:

Empirical data show that a significant number of software failures are induced by the interaction of two or more factors, and interaction faults can be extremely difficult to identify. Thus it is useful to measure the proportion of 2- way, 3-way, and higher strength combinations that are covered by a test set. Any combinations that have not been tested represent a portion of the input space for which the application has not been shown to be correct. Measuring the proportion of the input space for which the system response is untested and unknown can thus provide a useful quantity in estimating residual risk after testing. This poster explains the concept of combinatorial coverage measurement, a variety of measures that are available, and theorems relating (static) combinatorial coverage to (dynamic) structural coverage. These concepts are illustrated with examples comparing measures of tests for a NASA spacecraft and open source test configurations for the TLS cipher suite.

A configuration with n variables contains 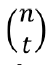 t-way combinations, so a test set with many configurations will contain a large number of combinations. Combinatorial coverage measures the inclusions of t-way combinations in a test set. Note that this measure is different from conventional structural coverage metrics (such as statement or branch coverage) and is independent of these other measures. Because combinatorial coverage measures the input space that is tested, and consequently also the untested portion of input space, it is useful in gauging the residual risk after testing.

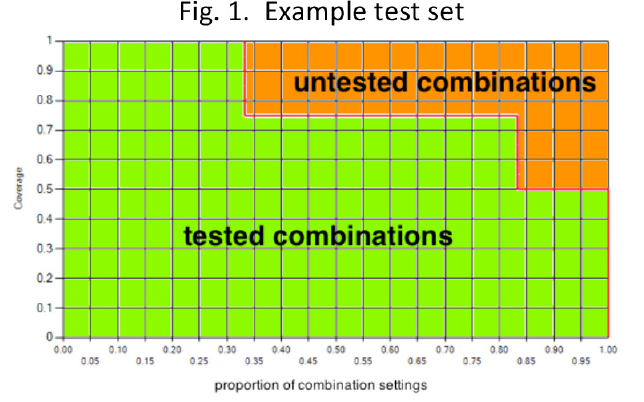
A variety of combinatorial coverage measures are available, including a fundamental measure of total variable-value configuration coverage: for a given combination of t variables, the proportion of all t-way value settings that are covered by at least one test case in a test set. For example, two binary variables have four possible settings. Consider four tests containing variables a, b, c, and d: {0000, 0110, 1001, 0111}. 
There are (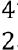 = 6 ) possible variable combinations and 22x 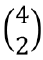= 24 possible variable-value configurations. Of these, 19 variable-value configurations are covered and the only ones missing are ab=11, ac=11, ad=10, bc=01, bc=10, so the total variable-value configuration coverage is 19/24 = 79 These measures are shown in Figure 1, where the upper right-hand corner represents the 21% of the 2-way combinations in the input space not tested.

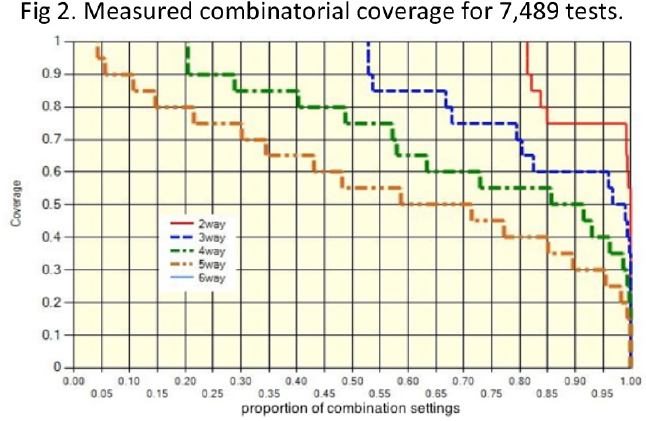
Figure 2 shows measurements for 2-way through 5-way combination  coverage  for 7,489 tests for a NASA spacecraft. Note that the untested portion for 2-way combinations (above red line) is only about 6% of the total, and 3-way to 5-way coverage is relatively high.

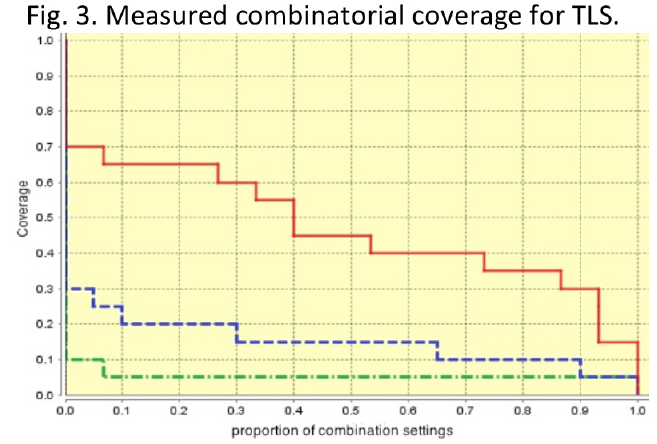
Now compare the measured test configurations for open source tests of the TLS cipher suite in Fig. 3. Less than half of the 2-way combinations are tested, and virtually none for 3-way and 4-way combinations, representing areas of the input space where its configurations are uncovered and could pose significant residual risk.

References:

D.     Kuhn, I. Dominguez Mendoza, R. Kacker, and Y. Lei, “Combinatorial  coverage measurement concepts and applications,” in Software Testing, Verification and Validation (ICSTW), 2013 IEEE 6th Intl Conf, pp. 352–361.

K.     Kleine, D. Simos, “Coverage analysis of subsets of the TLS cipher suite registry”, SBA Research, Oct. 1, 2015.

Bio:

Rick Kuhn is a computer scientist in the Computer Security Division of the National Institute of Standards and Technology. He has authored more than 100 publications on information security, empirical studies of software failure, and software assurance, and is a senior member of the IEEE. He co-developed the role based access control model (RBAC) used throughout industry and led the effort establishing RBAC as an ANSI standard. Before joining NIST, he worked as a systems analyst with NCR Corporation and the Johns Hopkins University Applied Physics Laboratory. He received an MS in computer science from the University of Maryland College Park.